簡単なデジタルフィルタの実装

プログラムでデジタル楽器やエフェクターなどの作成を作成していると、必ず必要になってくるのがデジタルフィルタ(ローパスフィルタやハイパスフィルタ等)です。

しかし、「1,000Hz以下を通すローパスフィルタがほしい」等と思って、いざデジタルフィルタを実装しようとすると、フィルタ設計(フィルタ係数の算出)の部分で「Z変換」や「伝達関数」といった高度な数学での説明が始まります。

この時点でハードルが高く、デジタル楽器やエフェクターの作成をあきらめてしまう人が多いのではないでしょうか？

ここではよく利用するデジタルフィルタについて、極力高度な数学を使わず簡単にフィルタ設計(フィルタ係数算出)・実装できる方法がありましたので紹介させていただきます。

今回の内容をC++のクラスとして簡単にまとめたものはこちらにあります。　→　簡単なデジタルフィルタのサンプルコード

Robert Bristow-Johnson Audio EQ Cookbook

簡単にフィルタ設計・実装する方法はRobert Bristow-Johnsonという方が「RBJ Audio EQ Cookbook」というテキストにまとめております。

「RBJ Audio EQ Cookbook」では、双2次(BiQuad)フィルタ(後述)とよばれるタイプのフィルタに対して、下記のフィルタ係数の求め方をまとめております。

ローパスフィルタ
ハイパスフィルタ
バンドパスフィルタ
ノッチフィルタ
ローシェルフフィルタ
ハイシェルフフィルタ
ピーキングフィルタ
オールパスフィルタ

それぞれのフィルタに対して、下記のパラメーターを決めて、「RBJ Audio EQ Cookbook」に記載された計算方法で計算をすれば、簡単にフィルタ係数が求められます。(フィルタ係数の計算方法については後述します。)

サンプリング周波数(単位：Hz)
カットオフ周波数(単位：Hz)
フィルタのQ値
帯域幅(単位：octave)
増幅量(単位：dB)

　※フィルタの種類によっては使わないパラメーターがあります。

双2次(BiQuad)フィルタ

双2次(BiQuad)フィルタは入力信号に対して2つ前までの入力信号と2つ前までの出力信号を使用して出力信号を計算するデジタルフィルタになります。
双2次(BiQuad)フィルタの詳細については省略いたします。C/C++で実装する場合、下記のようなイメージになります。

【実装イメージ】

// それぞれの変数は下記のとおりとする
// 　float input[]  …入力信号の格納されたバッファ。
// 　flaot output[] …フィルタ処理した値を書き出す出力信号のバッファ。
// 　int   size     …入力信号・出力信号のバッファのサイズ。
// 　float in1, in2, out1, out2  …フィルタ計算用のバッファ変数。初期値は0。
// 　float a0, a1, a2, b0, b1, b2 …フィルタの係数。 別途算出する。
for(int i = 0; i < size; i++)
{
	// 入力信号にフィルタを適用し、出力信号として書き出す。
	output[i] = b0/a0 * input[i] + b1/a0 * in1  + b2/a0 * in2
	                             - a1/a0 * out1 - a2/a0 * out2;

	in2  = in1;       // 2つ前の入力信号を更新
	in1  = input[i];  // 1つ前の入力信号を更新

	out2 = out1;      // 2つ前の出力信号を更新
	out1 = output[i]; // 1つ前の出力信号を更新
}

// それぞれの変数は下記のとおりとする

// 　float input[] …入力信号の格納されたバッファ。

// 　flaot output[] …フィルタ処理した値を書き出す出力信号のバッファ。

// 　int size …入力信号・出力信号のバッファのサイズ。

// 　float in1, in2, out1, out2 …フィルタ計算用のバッファ変数。初期値は0。

// 　float a0, a1, a2, b0, b1, b2 …フィルタの係数。別途算出する。

for(int i = 0; i < size; i++)

{

// 入力信号にフィルタを適用し、出力信号として書き出す。

output[i] = b0/a0 * input[i] + b1/a0 * in1 + b2/a0 * in2

- a1/a0 * out1 - a2/a0 * out2;

in2 = in1; // 2つ前の入力信号を更新

in1 = input[i]; // 1つ前の入力信号を更新

out2 = out1; // 2つ前の出力信号を更新

out1 = output[i]; // 1つ前の出力信号を更新

}

RBJ Audio EQ Cookbookによるフィルタ係数の求め方

フィルタ係数(a0～a2、b0～b2)の求め方は前述の各パラメータを元にRBJ Audio EQ Cookbookに記載された式に当てはめれば求めることができます。
各フィルタごとに使用するパラメータや計算方法が違うのでそれぞれのフィルタでのフィルタ係数の求め方について記載いたします。

ローパスフィルタ

ローパスフィルタは、カットオフ周波数以下の音声のみを通すフィルタです。下記の3つのパラメータを使用します。

サンプリング周波数(単位：Hz)
カットオフ周波数(単位：Hz)
フィルタのQ値

フィルタ係数の求め方は下記の通りです。(C/C++コードイメージ)

// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float q    … フィルタのQ値
float omega = 2.0f * 3.14159265f *  freq　/　samplerate;
float alpha = sin(omega) / (2.0f * q);

float a0 =  1.0f + alpha;
float a1 = -2.0f * cos(omega);
float a2 =  1.0f - alpha;
float b0 = (1.0f - cos(omega)) / 2.0f;
float b1 =  1.0f - cos(omega);
float b2 = (1.0f - cos(omega)) / 2.0f;

// それぞれの変数は下記のとおりとする

// float samplerate … サンプリング周波数

// float freq … カットオフ周波数

// float q … フィルタのQ値

float omega = 2.0f * 3.14159265f * freq　/　samplerate;

float alpha = sin(omega) / (2.0f * q);

float a0 = 1.0f + alpha;

float a1 = -2.0f * cos(omega);

float a2 = 1.0f - alpha;

float b0 = (1.0f - cos(omega)) / 2.0f;

float b1 = 1.0f - cos(omega);

float b2 = (1.0f - cos(omega)) / 2.0f;

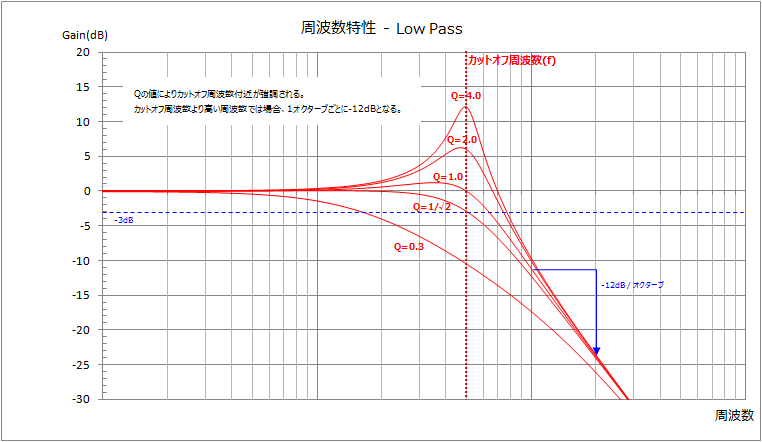
カットオフ周波数はそれ以上の周波数を通さなくする周波数です。(厳密には出力信号が-3dBとなる周波数。カットオフ周波数より低い周波数から減衰が始まります。)
Q値を大きくすることでカットオフ周波数でのGainの減少を抑えることができますが、大きくしすぎるとカットオフ周波数付近がが強調されてしまいます。(シンセサイザーのレゾナンスのような効果がかかります。)
カットオフ周波数付近を強調したくない場合は、Q値を1/√2にします。なお、Q値は0より大きい値でなければなりません。

ハイパスフィルタ

ハイパスフィルタは、カットオフ周波数以上の音声のみを通すフィルタです。下記の3つのパラメータを使用します。

サンプリング周波数(単位：Hz)
カットオフ周波数(単位：Hz)
フィルタのQ値

フィルタ係数の求め方は下記の通りです。(C/C++コードイメージ)

// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float q    … フィルタのQ値
float omega = 2.0f * 3.14159265f *  freq　/　samplerate;
float alpha = sin(omega) / (2.0f * q);

float a0 =   1.0f + alpha;
float a1 =  -2.0f * cos(omega);
float a2 =   1.0f - alpha;
float b0 =  (1.0f + cos(omega)) / 2.0f;
float b1 = -(1.0f + cos(omega));
float b2 =  (1.0f + cos(omega)) / 2.0f;

// それぞれの変数は下記のとおりとする

// float samplerate … サンプリング周波数

// float freq … カットオフ周波数

// float q … フィルタのQ値

float omega = 2.0f * 3.14159265f * freq　/　samplerate;

float alpha = sin(omega) / (2.0f * q);

float a0 = 1.0f + alpha;

float a1 = -2.0f * cos(omega);

float a2 = 1.0f - alpha;

float b0 = (1.0f + cos(omega)) / 2.0f;

float b1 = -(1.0f + cos(omega));

float b2 = (1.0f + cos(omega)) / 2.0f;

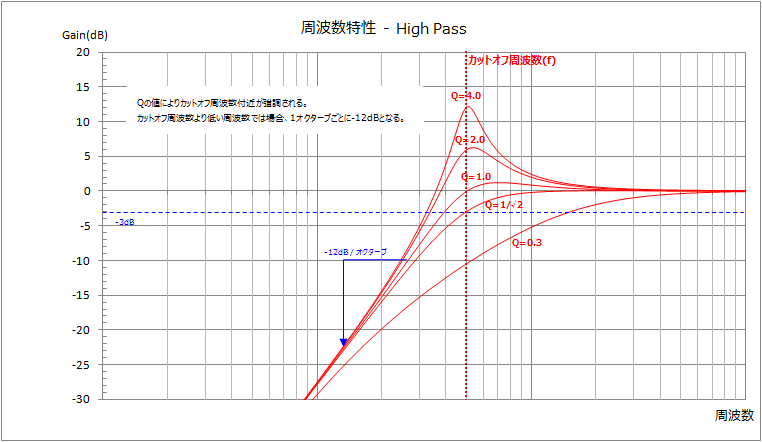
カットオフ周波数はそれ以下の周波数を通さなくする周波数です。(厳密には出力信号が-3dBとなる周波数。カットオフ周波数より高い周波数から減衰が始まります。)
Q値を大きくすることでカットオフ周波数でのGainの減少を抑えることができますが、大きくしすぎるとカットオフ周波数付近がが強調されてしまいます。(シンセサイザーのレゾナンスのような効果がかかります。)
カットオフ周波数付近を強調したくない場合は、Q値を1/√2にします。なお、Q値は0より大きい値でなければなりません。

バンドパスフィルタ

バンドパスフィルタは、カットオフ周波数を中心とし帯域幅分の音声のみを通すフィルタです。下記の3つのパラメータを使用します。

サンプリング周波数(単位：Hz)
カットオフ周波数(単位：Hz)
帯域幅(単位：octave)

フィルタ係数の求め方は下記の通りです。(C/C++コードイメージ)

// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float bw   … 帯域幅
float omega = 2.0f * 3.14159265f *  freq　/　samplerate;
float alpha = sin(omega) * sinh(log(2.0f) / 2.0 * bw * omega / sin(omega));

float a0 =  1.0f + alpha;
float a1 = -2.0f * cos(omega);
float a2 =  1.0f - alpha;
float b0 =  alpha;
float b1 =  0.0f;
float b2 = -alpha;

// それぞれの変数は下記のとおりとする

// float samplerate … サンプリング周波数

// float freq … カットオフ周波数

// float bw … 帯域幅

float omega = 2.0f * 3.14159265f * freq　/　samplerate;

float alpha = sin(omega) * sinh(log(2.0f) / 2.0 * bw * omega / sin(omega));

float a0 = 1.0f + alpha;

float a1 = -2.0f * cos(omega);

float a2 = 1.0f - alpha;

float b0 = alpha;

float b1 = 0.0f;

float b2 = -alpha;

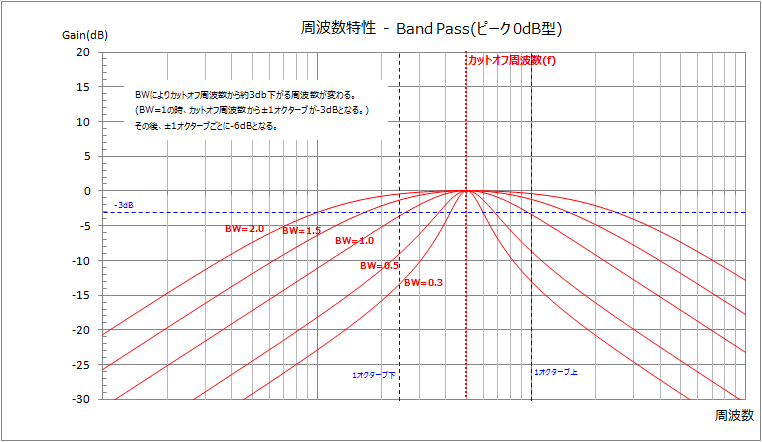
カットオフ周波数は通す帯域の中心となる周波数です。帯域幅はカットオフ周波数からどこまでの周波数を通すかを指定します。(厳密には出力信号が-3dBとなる周波数。)
例えば、カットオフ周波数が440Hzで帯域幅が1オクターブなら、220Hz～880Hzで、2オクターブなら110Hz～1760Hzが通す周波数となります。
なお、帯域幅は0より大きい値でなければなりません。

ノッチフィルタ

ノッチフィルタは、カットオフ周波数を中心とした帯域幅分の音声以外を通すフィルタです。下記の3つのパラメータを使用します。

サンプリング周波数(単位：Hz)
カットオフ周波数(単位：Hz)
帯域幅(単位：octave)

フィルタ係数の求め方は下記の通りです。(C/C++コードイメージ)

// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float bw   … 帯域幅
float omega = 2.0f * 3.14159265f *  freq　/　samplerate;
float alpha = sin(omega) * sinh(log(2.0f) / 2.0 * bw * omega / sin(omega));

float a0 =  1.0f + alpha;
float a1 = -2.0f * cos(omega);
float a2 =  1.0f - alpha;
float b0 =  1.0f;
float b1 = -2.0f * cos(omega);
float b2 =  1.0f;

// それぞれの変数は下記のとおりとする

// float samplerate … サンプリング周波数

// float freq … カットオフ周波数

// float bw … 帯域幅

float omega = 2.0f * 3.14159265f * freq　/　samplerate;

float alpha = sin(omega) * sinh(log(2.0f) / 2.0 * bw * omega / sin(omega));

float a0 = 1.0f + alpha;

float a1 = -2.0f * cos(omega);

float a2 = 1.0f - alpha;

float b0 = 1.0f;

float b1 = -2.0f * cos(omega);

float b2 = 1.0f;

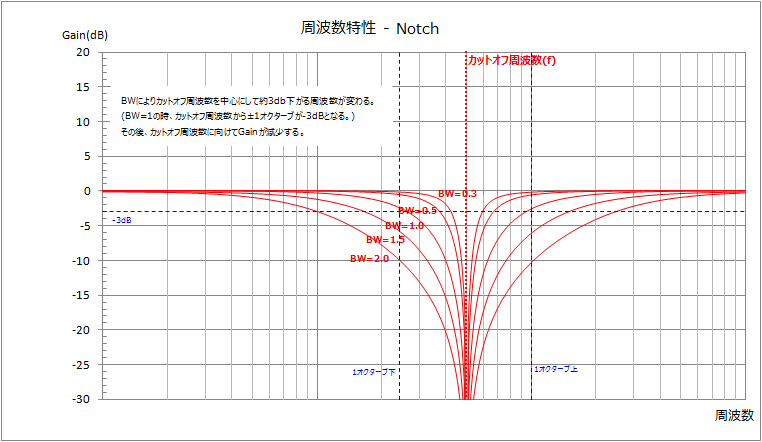
カットオフ周波数は通さない帯域の中心となる周波数です。帯域幅はカットオフ周波数からどこまでの周波数を通さないかを指定します。(厳密には出力信号が-3dBとなる周波数。)
例えば、カットオフ周波数が440Hzで帯域幅が1オクターブなら、220Hz～880Hzで、2オクターブなら110Hz～1760Hzが通さない周波数となります。
なお、帯域幅は0より大きい値でなければなりません。

ローシェルフフィルタ

ローシェルフフィルタは、カットオフ周波数以下の音声を増幅量分だけ増幅するフィルタです。下記の4つのパラメータを使用します。

サンプリング周波数(単位：Hz)
カットオフ周波数(単位：Hz)
フィルタのQ値
増幅量(単位：dB)

フィルタ係数の求め方は下記の通りです。(C/C++コードイメージ)

// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float q    … フィルタのQ値
// float gain … 増幅量
float omega = 2.0f * 3.14159265f *  freq　/　samplerate;
float alpha = sin(omega) / (2.0f * q);
float A     = pow(10.0f, (gain / 40.0f) );
float beta  = sqrt(A) / q;

float a0 = (A + 1.0f)+(A - 1.0f) * cos(omega) + beta * sin(omega);
float a1 = -2.0f * ((A - 1.0f) + (A + 1.0f) * cos(omega));
float a2 = (A + 1.0f) + (A - 1.0f) * cos(omega) - beta * sin(omega);
float b0 =  A * ((A + 1.0f) - (A - 1.0f) * cos(omega) + beta * sin(omega));
float b1 =  2.0f * A * ((A - 1.0f) - (A + 1.0f) * cos(omega));
float b2 =  A * ((A + 1.0f) - (A-  1.0f) * cos(omega) - beta * sin(omega));

// それぞれの変数は下記のとおりとする

// float samplerate … サンプリング周波数

// float freq … カットオフ周波数

// float q … フィルタのQ値

// float gain … 増幅量

float omega = 2.0f * 3.14159265f * freq　/　samplerate;

float alpha = sin(omega) / (2.0f * q);

float A = pow(10.0f, (gain / 40.0f) );

float beta = sqrt(A) / q;

float a0 = (A + 1.0f)+(A - 1.0f) * cos(omega) + beta * sin(omega);

float a1 = -2.0f * ((A - 1.0f) + (A + 1.0f) * cos(omega));

float a2 = (A + 1.0f) + (A - 1.0f) * cos(omega) - beta * sin(omega);

float b0 = A * ((A + 1.0f) - (A - 1.0f) * cos(omega) + beta * sin(omega));

float b1 = 2.0f * A * ((A - 1.0f) - (A + 1.0f) * cos(omega));

float b2 = A * ((A + 1.0f) - (A- 1.0f) * cos(omega) - beta * sin(omega));

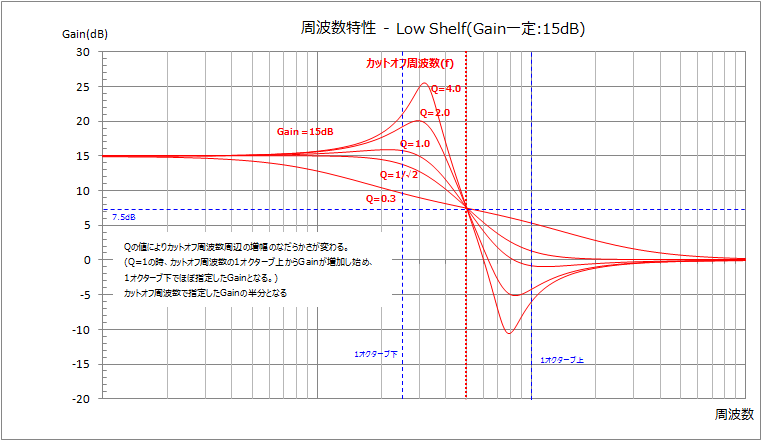
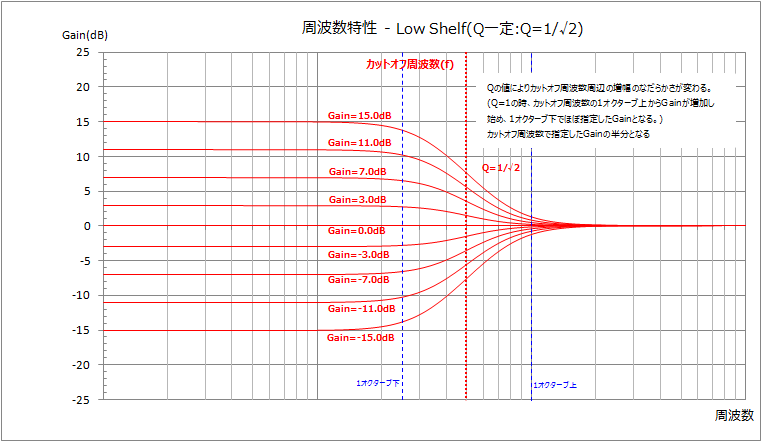
カットオフ周波数はそれ以下の周波数を増幅する周波数です。(厳密には出力信号が指定した増幅量の半分となる周波数。カットオフ周波数より高い周波数から増幅が始まります。)
増幅量をマイナスにするとカットオフ周波数以下の周波数を減衰させるフィルタになります。
Q値により、増幅のカーブを変更することができますが、大きくしすぎるとカットオフ周波数付近がが強調されてしまいます。
カットオフ周波数付近を強調したくない場合は、Q値を1/√2にします。なお、Q値は0より大きい値でなければなりません。

ハイシェルフフィルタ

ハイシェルフフィルタは、カットオフ周波数以上の音声を増幅量分だけ増幅するフィルタです。下記の4つのパラメータを使用します。

サンプリング周波数(単位：Hz)
カットオフ周波数(単位：Hz)
フィルタのQ値
増幅量(単位：dB)

フィルタ係数の求め方は下記の通りです。(C/C++コードイメージ)

// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float q    … フィルタのQ値
// float gain … 増幅量
float omega = 2.0f * 3.14159265f *  freq　/　samplerate;
float alpha = sin(omega) / (2.0f * q);
float A     = pow(10.0f, (gain / 40.0f) );
float beta  = sqrt(A) / q;

float a0 = (A + 1.0f) - (A - 1.0f) * cos(omega) + beta * sin(omega);
float a1 =  2.0f * ((A - 1.0f) - (A + 1.0f) * cos(omega));
float a2 = (A + 1.0f) - (A - 1.0f) * cos(omega) - beta * sin(omega);
float b0 =  A * ((A + 1.0f) + (A - 1.0f) * cos(omega) + beta * sin(omega));
float b1 = -2.0f * A * ((A - 1.0f) + (A + 1.0f) * cos(omega));
float b2 =  A * ((A + 1.0f) + (A - 1.0f) * cos(omega) - beta * sin(omega));

// それぞれの変数は下記のとおりとする

// float samplerate … サンプリング周波数

// float freq … カットオフ周波数

// float q … フィルタのQ値

// float gain … 増幅量

float omega = 2.0f * 3.14159265f * freq　/　samplerate;

float alpha = sin(omega) / (2.0f * q);

float A = pow(10.0f, (gain / 40.0f) );

float beta = sqrt(A) / q;

float a0 = (A + 1.0f) - (A - 1.0f) * cos(omega) + beta * sin(omega);

float a1 = 2.0f * ((A - 1.0f) - (A + 1.0f) * cos(omega));

float a2 = (A + 1.0f) - (A - 1.0f) * cos(omega) - beta * sin(omega);

float b0 = A * ((A + 1.0f) + (A - 1.0f) * cos(omega) + beta * sin(omega));

float b1 = -2.0f * A * ((A - 1.0f) + (A + 1.0f) * cos(omega));

float b2 = A * ((A + 1.0f) + (A - 1.0f) * cos(omega) - beta * sin(omega));

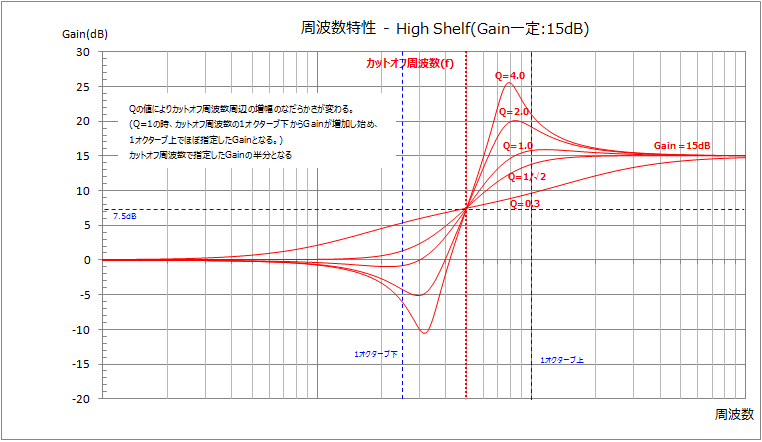
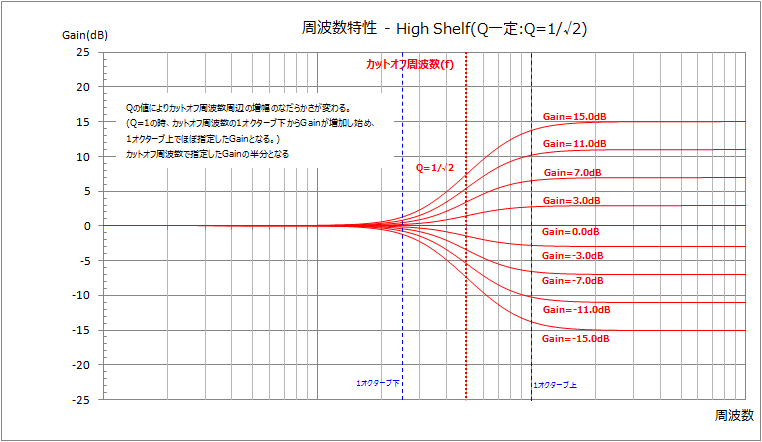
カットオフ周波数はそれ以上の周波数を増幅する周波数です。(厳密には出力信号が指定した増幅量の半分となる周波数。カットオフ周波数より低い周波数から増幅が始まります。)
増幅量をマイナスにするとカットオフ周波数以上の周波数を減衰させるフィルタになります。
Q値により、増幅のカーブを変更することができますが、大きくしすぎるとカットオフ周波数付近がが強調されてしまいます。
カットオフ周波数付近を強調したくない場合は、Q値を1/√2にします。なお、Q値は0より大きい値でなければなりません。

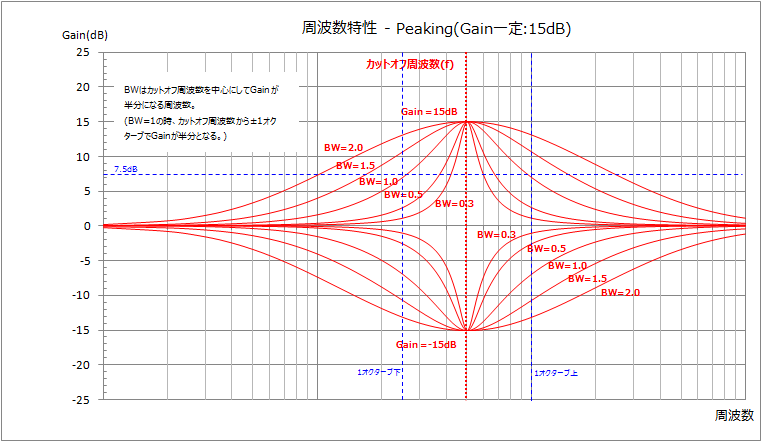
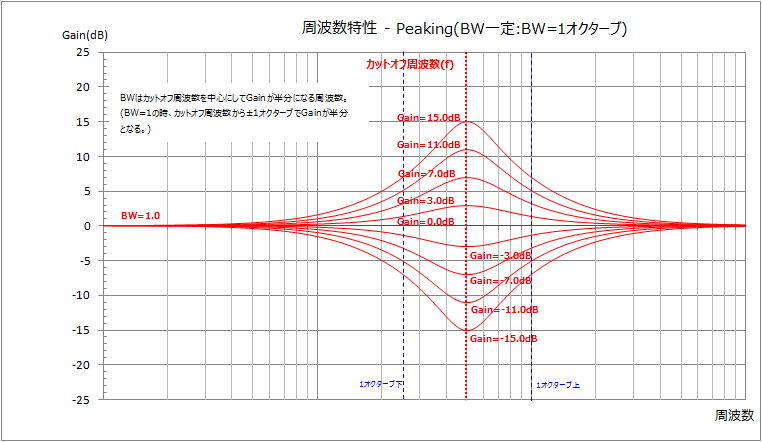
ピーキングフィルタ

ピーキングフィルタは、カットオフ周波数を中心とした帯域幅分の音声を増幅量分だけ増幅するフィルタです。下記の4つのパラメータを使用します。

サンプリング周波数(単位：Hz)
カットオフ周波数(単位：Hz)
帯域幅(単位：octave)
増幅量(単位：dB)

フィルタ係数の求め方は下記の通りです。(C/C++コードイメージ)

// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float q    … フィルタのQ値
// float gain … 増幅量
float omega = 2.0f * 3.14159265f *  freq　/　samplerate;
float alpha = sin(omega) * sinh(log(2.0f) / 2.0 * bw * omega / sin(omega));
float A     = pow(10.0f, (gain / 40.0f) );

float a0 =  1.0f + alpha / A;
float a1 = -2.0f * cos(omega);
float a2 =  1.0f - alpha / A;
float b0 =  1.0f + alpha * A;
float b1 = -2.0f * cos(omega);
float b2 =  1.0f - alpha * A;

// それぞれの変数は下記のとおりとする

// float samplerate … サンプリング周波数

// float freq … カットオフ周波数

// float q … フィルタのQ値

// float gain … 増幅量

float omega = 2.0f * 3.14159265f * freq　/　samplerate;

float alpha = sin(omega) * sinh(log(2.0f) / 2.0 * bw * omega / sin(omega));

float A = pow(10.0f, (gain / 40.0f) );

float a0 = 1.0f + alpha / A;

float a1 = -2.0f * cos(omega);

float a2 = 1.0f - alpha / A;

float b0 = 1.0f + alpha * A;

float b1 = -2.0f * cos(omega);

float b2 = 1.0f - alpha * A;

カットオフ周波数は増幅する帯域の中心となる周波数です。帯域幅はカットオフ周波数からどこまでの周波数を通すかを指定します。(厳密には出力信号が指定した増幅量の半分となる周波数。)
増幅量をマイナスにするとカットオフ周波数周辺の音声を減衰させるフィルタになります。
例えば、カットオフ周波数が440Hzで帯域幅が1オクターブなら、220Hz～880Hzで、2オクターブなら110Hz～1760Hzが増幅する周波数となります。
なお、帯域幅は0より大きい値でなければなりません。

オールパスフィルタ

オールパスフィルタは、カットオフ周波数周辺の位相のみを変えます。下記の3つのパラメータを使用します。

サンプリング周波数(単位：Hz)
カットオフ周波数(単位：Hz)
フィルタのQ値

フィルタ係数の求め方は下記の通りです。(C/C++コードイメージ)

// それぞれの変数は下記のとおりとする
// float samplerate … サンプリング周波数
// float freq … カットオフ周波数
// float q    … フィルタのQ値
float omega = 2.0f * 3.14159265f *  freq　/　samplerate;
float alpha = sin(omega) / (2.0f * q);

float a0 =  1.0f + alpha;
float a1 = -2.0f * cos(omega);
float a2 =  1.0f - alpha;
float b0 =  1.0f - alpha;
float b1 = -2.0f * cos(omega);
float b2 =  1.0f + alpha;

// それぞれの変数は下記のとおりとする

// float samplerate … サンプリング周波数

// float freq … カットオフ周波数

// float q … フィルタのQ値

float omega = 2.0f * 3.14159265f * freq　/　samplerate;

float alpha = sin(omega) / (2.0f * q);

float a0 = 1.0f + alpha;

float a1 = -2.0f * cos(omega);

float a2 = 1.0f - alpha;

float b0 = 1.0f - alpha;

float b1 = -2.0f * cos(omega);

float b2 = 1.0f + alpha;

Q値は0より大きい値でなければなりません。
このフィルタはあまり使用する機会はないと思われます。(フェイザーやリバーブなどで使われます。)

周波数特性については省略します。

サンプルコード(ローパスフィルタ)

ローパスフィルタを適用する関数の例を下記に記載いたします。

なお、本サイトではVSTプラグイン作成を視野に入れていますので、入力信号・出力信号はfloat型としております。
WAVファイル等に適用するためにint型やshort型等の整数型を使用される場合は、型をキャストして利用してください。

また、フィルタ係数もfloat型としておりますが、もちろんdouble型でもかまいません。

// float input[]  …入力信号の格納されたバッファ。
// flaot output[] …フィルタ処理した値を書き出す出力信号のバッファ。
// int   size     …入力信号・出力信号のバッファのサイズ。
// float samplerate … サンプリング周波数。
// float freq … カットオフ周波数。
// float q    … フィルタのQ値。
void lowpass(float input[], float output[], int size, float samplerate, float freq, float q)
{
	// フィルタ係数を計算する
	float omega = 2.0f * 3.14159265f *  freq　/　samplerate;
	float alpha = sin(omega) / (2.0f * q);

	float a0 =  1.0f + alpha;
	float a1 = -2.0f * cos(omega);
	float a2 =  1.0f - alpha;
	float b0 = (1.0f - cos(omega)) / 2.0f;
	float b1 =  1.0f - cos(omega);
	float b2 = (1.0f - cos(omega)) / 2.0f;

	// フィルタ計算用のバッファ変数。
	float in1  = 0.0f;
	float in2  = 0.0f;
	float out1 = 0.0f;
	float out2 = 0.0f;

	// フィルタを適用
	for(int i = 0; i < size; i++)
	{
		// 入力信号にフィルタを適用し、出力信号として書き出す。
		output[i] = b0/a0 * input[i] + b1/a0 * in1  + b2/a0 * in2
		                             - a1/a0 * out1 - a2/a0 * out2;

		in2  = in1;       // 2つ前の入力信号を更新
		in1  = input[i];  // 1つ前の入力信号を更新

		out2 = out1;      // 2つ前の出力信号を更新
		out1 = output[i]; // 1つ前の出力信号を更新
	}
}

// float input[] …入力信号の格納されたバッファ。

// flaot output[] …フィルタ処理した値を書き出す出力信号のバッファ。

// int size …入力信号・出力信号のバッファのサイズ。

// float samplerate … サンプリング周波数。

// float freq … カットオフ周波数。

// float q … フィルタのQ値。

void lowpass(float input[], float output[], int size, float samplerate, float freq, float q)

{

// フィルタ係数を計算する

float omega = 2.0f * 3.14159265f * freq　/　samplerate;

float alpha = sin(omega) / (2.0f * q);

float a0 = 1.0f + alpha;

float a1 = -2.0f * cos(omega);

float a2 = 1.0f - alpha;

float b0 = (1.0f - cos(omega)) / 2.0f;

float b1 = 1.0f - cos(omega);

float b2 = (1.0f - cos(omega)) / 2.0f;

// フィルタ計算用のバッファ変数。

float in1 = 0.0f;

float in2 = 0.0f;

float out1 = 0.0f;

float out2 = 0.0f;

// フィルタを適用

for(int i = 0; i < size; i++)

{

// 入力信号にフィルタを適用し、出力信号として書き出す。

output[i] = b0/a0 * input[i] + b1/a0 * in1 + b2/a0 * in2

- a1/a0 * out1 - a2/a0 * out2;

in2 = in1; // 2つ前の入力信号を更新

in1 = input[i]; // 1つ前の入力信号を更新

out2 = out1; // 2つ前の出力信号を更新

out1 = output[i]; // 1つ前の出力信号を更新

}

フィルタの実装例とエフェクター実装例

参考までにここで説明したフィルタについてクラス化したものを下記に記載しております。
→簡単なデジタルフィルタのサンプルコード

また、上記のフィルタクラスを利用したエフェクターの実装例なども下記に記載しております。
→エフェクターの実装例

最後に

ここでは各フィルタの特性や詳細は、あえてふれずに実装方法を簡単に紹介させていただきました。
これを使用すればエフェクターやデジタル楽器の作成がよりやりやすくなるかと思います。

なお、ここで紹介した係数の計算方法や実装方法は一例でしかありません。
バンドパスフィルタやノッチフィルタでは帯域幅の代わりにQを利用したり、ローシェルフフィルタやハイシェルフフィルタではQの代わりにスロープというパラメータを利用することもできます。
フィルタ特性や詳細な内容について知りたい方は、検索やより詳細に記載されている参考サイト様等でご確認いただければと思います。

参考サイト様

MusicDSP 様 – Audio-EQ-Cookbook(英語)
https://www.musicdsp.org/files/Audio-EQ-Cookbook.txt

MusicDSP 様 – C++ class implementation of RBJ Filters(英語)
www.musicdsp.org/files/CFxRbjFilter.h

g200kg 様 – BiQuadフィルタの料理法
https://www.g200kg.com/jp/docs/makingeffects/78743dea3f70c8c2f081b7d5187402ec75e6a6b8.html

++C++;// 未確認飛行 C 様 – 双2次フィルタ
https://ufcpp.net/study/digital_filter/biquad.html

One thought on “簡単なデジタルフィルタの実装”

RORO より:

2015年7月11日 9:48 PM

大学でアナログセンサのフィルターを使うことになりましてこのサンプルコードを利用してもよろしいでしょうか？
また、大変恐縮ではありますが、Q値をどのくらいに設定したらよろしいのでしょうか？

返信
1. うつぼかずら@管理人 より:
  
  2015年7月12日 10:46 AM
  
  ROROさん
  
  サンプルコードは自己の責任にてご自由にご利用いただいて大丈夫です。
  
  ただ、ここで紹介しているフィルタは、音声信号処理用のフィルタです。
  センサとなるとそのまま適応できないかもしれません。
  
  Q値は「どのようなフィルタがほしいか？」によって異なってきますので、
  「どのぐらいに設定したらよいか？」についてはお答えしかねます。
  カットオフ周波数付近で強調が必要なら1.0以上、必要なければ0.7～1.0ぐらいで
  まずは試していただいてはいかがでしょうか？
  
  返信
  1. RORO より:
    
    2015年7月12日 4:14 PM
    
    ありがとうございます！
    無事に作成することが出来ました！
    qの値は1にして行いました。
    
    返信
kaoaru より:

2018年3月8日 10:23 AM

Ｃのソースコードイメージはわかりやすい。参考になります。ありがとうございます。

返信
1. うつぼかずら@管理人 より:
  
  2018年3月8日 6:36 PM
  
  kaoaruさん
  
  閲覧いただきありがとうございます。
  わかりやすいと言っていただけて非常に嬉しいです。
  
  返信
Ale より:

2019年1月22日 8:11 PM

電子機器のフィルタのソースコード見てもさっぱり分からず困っていたのですが、ここのサンプルコードのおかげでイメージがつきました。ありがとうございます。

返信
うつぼかずら@管理人 より:

2019年1月24日 11:25 PM

Aleさん
書き込みありがとうございます。イメージがつかめて良かったです。いろいろなフィルタがあると思いますので頑張ってください。

返信
hiro より:

2021年1月26日 3:52 PM

分かりやすい内容で、とても勉強になりました。
周波数特性の図は管理者様が作られたものなのでしょうか？
もし、何かを参考にしたのであれば、教えていただきたいです。

返信
1. うつぼかずら@管理人 より:
  
  2021年1月29日 6:32 PM
  
  hiroさん
  書き込みありがとうございます。
  周波数特性の図は私が作成しました。参考サイト様に周波数特性の式があるのでこちらをそのまま図にしたものになります。
  
  返信